Taleb's Statistical Consequences of Fat Tails: Chapter 3 Summary

The following post is a summary of Nassim Nicholas Taleb’s The Technical Incerto Collection: Chapter 3 - A Non-Technical Overview - The Darwin College Lecture.

Chapter 3 begins with an introduction to thin tailed distributions and thick tailed distributions. Taleb makes up the following imaginary domains Mediocristan (thin tails) and Extremistan (thick tails). In Mediocristan, extreme rare events do not have a significant impact on the statistical properties of the distribution. When you think Mediocristan, think about "normal" distributions from statistics class. For example, the height of all Americans. When sampling two Americans, if their combined height is 4.1 meters (very unlikely), the most likely combination of their two heights is 2.05 meters and 2.05 meters - not 10 centimeters and 4 meters.

Next, in thick tailed distributions, which Taleb calls Extremistan, extreme rare events have a disproportionate impact on the distribution. When you think about Extremistan, think about real life distributions with large outliers. For example, it's more likely that two people selected at random with a combined wealth of $36 million are split $35,999,000 and $1000 than $18M and $18M. Jeff Bezos’ wealth has a disproportionate impact on the mean wealth of Americans.

The distinction between these two worlds is as follows: in Mediocristan, in order to reach that unlikely of an outlier event (4.1 meters), you need the combination of two large events. In Extremistan, you can get to those unlikely outlier events with a single event ($35,999,000).

Extremistan distributions behave under Power Laws. When we typically learn statistics, we use the law of large numbers (LLN) definition as a shortcut. Essentially, the LLN says that if a distribution has a mean, you can sample A LOT of data and eventually get the mean of the population. A major premise of Taleb's book is that for fat tail distributions (Extremistan), it takes A LOT of data to make the law of large numbers reach the true population mean. However, in the real world, it is very difficult to get that amount of data.

A useful example of a power law is the "80/20" principle. This distribution (called the Pareto distribution) frequently loosely describes real phenomenon: 80% of the wealth is controlled by 20% of the population, 80% of customer service problems come from 20% of customers, 80% of beer is drank by 20% of beer drinkers. In these distributions, 92% of the observations fall below the true mean. As such, the large rare events disproportionately determine the mean. Jeff Bezos' wealth pulls the mean much higher than our wealth pulls the mean. A nation's wealth helps illustrate the "80/20" rule, but most economic metrics do not have the entirety of the population data like nation wealth data.

Since economic metrics do not have the entirety of the population data, it requires A LOT of data to find enough of those rare events that will drive the true mean of the population. As such, financial metrics that use means or standard deviations (Sharpe ratio and Beta) are likely misleading. They don't have enough data to take into account rare events like 2008 or COVID-19!

Another consequence of the failure to account for fat tails is that some forecasters will heavily rely on empirical data. Empirical data (known, visible data) fails to predict future maximums. For example, it's naive to build a building using the worst past flood level as your maximum exposure. "For thick tails, the difference between past maxima and future expected maxima is much larger than thin tails."

The need for large amounts of data for Extremistan distributions emphasizes the following point: absence of evidence does not equal evidence of absence. For example, saying world violence has dropped (absence of evidence) does not mean that violence has actually dropped. We do not know if there lies a rare, large impact event ahead of us (another World War) that would make that statement false. However, if another World War occurred, we could be very confident that violence has increased. "This is the negative empiricism that underpins Western science. As we gather information, we can rule things out." Remember when cigarette companies boasted for 50 years that there was no evidence that smoking is harmful? Same thing.

Next, Taleb explains how forecasting fails to consider the payoff related to events. When discussing forecasts, one cannot simply talk about the percent likelihood, but they must also consider the impact of that event ("payoff swamps probability"). For example, the likelihood of a global pandemic is low, but the impact to your portfolio is very high. Similarly, the likelihood of the '08 housing market collapse was low (few predicted it, though many claim in hindsight it was obvious), but the negative payoff was immense. Taleb often notes the entire banking system lost all the money they've ever made in 2008 and 2009. This is similar to the reason why you'd never play Russian roulette no matter how much money you'd receive for "winning." The negative payoff is just too high.

Credit Stefan Gasic.

Back to the Law of Large Numbers, Taleb focuses on a fundamental point of Extremistan - it requires much more data (10^11 observations) to stabilize the mean. I found the graph below to be the most helpful graph in this chapter. The first graph, a Gaussian distribution (Mediocristan) or something like the height of adults, stabilizes to find the mean height after 30 observations. You have a pretty good idea of the average height of adults after seeing a crowd. The second graph, a Pareto "80/20" distribution (Extremistan), takes many observations to find the mean. When 20% of Italians own 80% of the land, you have to sample many, many Italians to find the value of the mean land ownership percent.

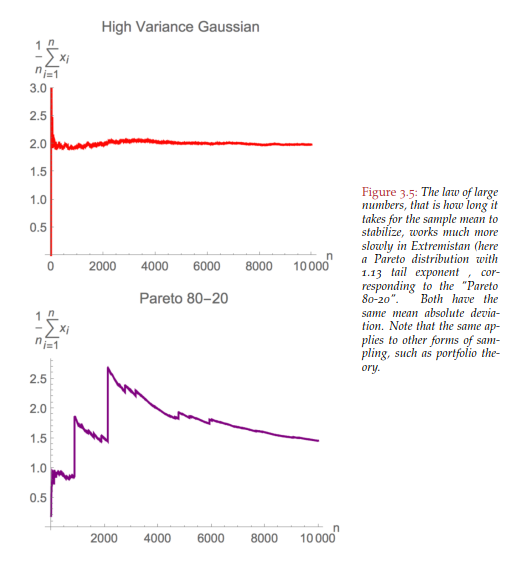
This leads to an important point in determining the appropriate distribution to fit to a data set. One should determine the distribution based on the process of elimination. This introduces the idea of a Black Swan. A black swan is a rare event - a big, impactful deviation from the normal. If you observe a Black Swan in the data set (say a 10 sigma event) you can now say the distribution is thick tailed (Extremistan) by elimination. You cannot certify that it is thin tailed because this 10 sigma event has appeared. Because of the Black Swan, you now know that you are living in Extremistan.

The idea of the Black Swan relates directly with the error to rely on observable "empirical" data to feel comfort that there were only 2 observed Ebola deaths in the US; therefore, we should be more worried about diabetes deaths or car crashes deaths. However, due to Ebola's distribution and the tail thickness, it should not be talked about in the same sentence as car crashes. See my full article about the risks of pandemics.

This brings us to the importance of understanding power law distributions (Extremistan). Taleb explains in more technical terms that a power law distribution (like the 80/20 Pareto distribution) does not have reliable "moments." To define moments: the first moment is the mean and the second moment is the variance. The largest observation of the S&P over the past 56 years accounted for 80% of the kurtosis (a function of the fourth moment & a measure of the amount of probability in the tails of the distribution). In short, this means that if one observation accounted for that much probability of the tails, we cannot trust the mean or variance. The mean and variance can move far too much with another large, rare event.

This again highlights the importance of determining the correct distribution of a data set. Once we determine the distribution, we can estimate the statistical mean using the information from the distribution type. This gives us a more accurate depiction of the mean rather than using "empirical" data that may be missing large impact, rare events.

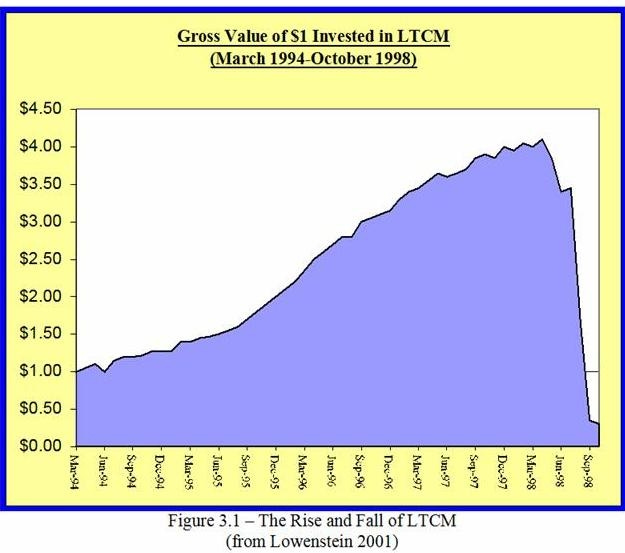
Taleb gives an example of determining the correct distribution using Long Term Capital Management (LTCM). LTCM was a hedge fund run by Nobel prize winners in the late 90's. When their leveraged fund collapsed and nearly brought down the financial system with it (thank the big banks for bailing them out), the founders blamed the collapse on a "10 sigma" event. Using a Gaussian (normal) distribution, the event "a ten sigma event" we describe as the survival function (probability of collapse) is 1 in 1.31 x 10^-23. However, using a Power Law distribution, the survival function is 1 in 203. In short, they used the wrong distribution when trying to explain that the chances of them collapsing were 1 in a bazillion.

Furthering the discussion of Black Swans, Taleb transitions to a variable X and the function of X or F(X). F(X) is the exposure or payoff related to X. We have much more control over the F(X). For example, X is changes in your wealth and F(X) is how this changes your well-being. We have less control over changes to our wealth than how it impacts our well-being. So, there is no way to predict Black Swans, but we can deal with Black Swans by controlling our exposure or payoff related to them. Exposure is more important than knowledge because we don't know what we don't know (no matter how smart we think we are).

Finally, the chapter concludes with ruin and path dependence. Previously a trader, Taleb is concerned about ruin - if you lose it all, you cannot continue to trade. As such, there should be an emphasis on surviving so you get to continue to play the game. See the example below for the difference between ensemble probability and time probability. In ensemble probability, if one person out of 100 dies riding a motorcycle today, the death rate is 1%. However, with time probability, if one motorcyclist rides every single day, their life expectancy decreases. I believe this highlights our evolutionary tendency to overreact and "panic" to low probability things that could kill us. Once you're dead, it's game over!

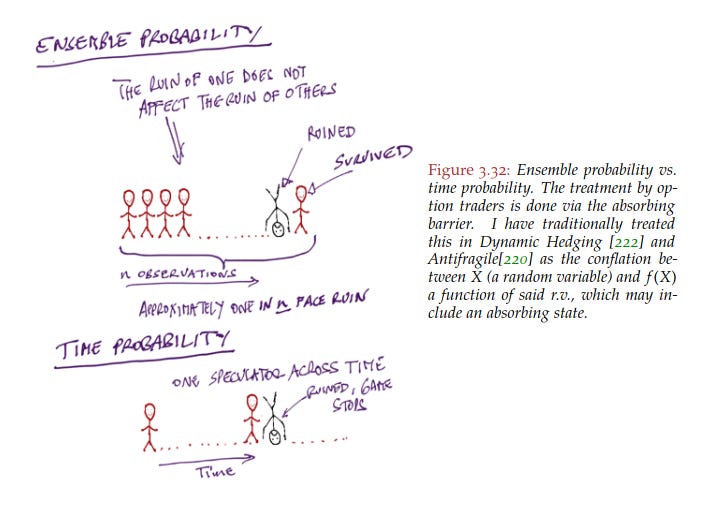
"To summarize, we first need to make a distinction between mediocristan and Extremistan, two separate domains that about never overlap with one another. If we fail to make that distinction, we don’t have any valid analysis. Second, if we don’t make the distinction between time probability (path dependent) and ensemble probability (path independent), we don’t have a valid analysis.”

Taleb offers valuable insight into statistics and probability. However, his writing goes further. My biggest takeaway is the importance of uncertainty in our lives. Especially given recent events around COVID-19, it’s important to understand uncertainty in our world. Taleb further talks about how to live in an uncertain world in the book Antifragile. In short, “Antifragile is beyond resilience or robustness. The resilient resists shocks and stays the same; the antifragile gets better.” What doesn’t kill you makes you stronger.